Why's my program slow?
Algorithmic Complexity and You
Note
http://www.vrplumber.com/programming/runsnakerun/ http://bigocheatsheet.com/ http://accidentallyquadratic.tumblr.com/
advanced algorithms resources: https://gist.github.com/debasishg/8172796
Algorithmic Complexity and You
Note
http://www.vrplumber.com/programming/runsnakerun/ http://bigocheatsheet.com/ http://accidentallyquadratic.tumblr.com/
advanced algorithms resources: https://gist.github.com/debasishg/8172796
These slides are online at:
http://talks.edunham.net/linuxfestnorthwest2015/complexity/
Note
Before upper-division CS classes, I thought there was some kind of secret sauce and complexity was super scary
Afterwards it's clear how simple things are, so much that the core concepts can fit into an hour at a conference
The difficulty is in the details, and this stuff is still indescribably tough to implement at the compiler level, but understanding the high-level view can help you ask smart questions and better understand real-world code
Note
before I took algorithms classes at OSU, I thought complexity was secret magic that only "real computer scientists" could understand... afterwards it looked like common sense
not everybody in the real world gets the academic side; not everyone in academia gets the real-world side; i'm here to teach you about both
In Theory
In Practice
Note
scope of this talk will be small though available knowledge is vast
jumping into the graduate level stuff here would be like a talk on getting started with recreational hiking focusing on what to take for a month in the Alps, rather than focusing on what to pack for a picnic in a nearby park
Note
Why do they have time for a sword fight while the compiler runs?
There are two factors: The compiler has to do many operations (this scales with how big a program you compile) and each operation takes some time (this is something which can be optimized in the compiler)
Note
How long does your code take to run?
"About 2 minutes to compile"?
"About half an hour to run all the tests"?
NEXT: in terms of input size
n is the size of the input.
N: /N/, quant.
- A large and indeterminate number of objects: “There were N bugs in that
crock!” Also used in its original sense of a variable name: “This crock has N bugs, as N goes to infinity.”
O(n)
(time in loop) * (times the loop runs) + (time outside of loop)
Note
Not like C the language; C like a constant amount of time
O(n)
Sound smarter? And write less? Win-Win!
Graph of why it's "usually ok to omit the constant" (more on that later)
Note
http://www.cs.cmu.edu/~adamchik/15-121/lectures/Algorithmic%20Complexity/complexity.html
monotonic = always-increasing or always-decreasing
For any monotonic functions f(n) and g(n) from the positive integers to the positive integers, we say that f(n) = O(g(n)) when there exist constants c > 0 and n[0] > 0 such that:
f(n) ≤ c * g(n), for all n ≥ n[0]
Note
How many of you really understood the P vs NP thing?
"NP problems are really 'hard', P problems are 'solvable'"
P is problems that can be SOLVED in polynomial time
NP is problems that can be VERIFIED in polynomial time
x^2 is polynomial; 2^x is exponential
Traveling salesman by brute force (shortest route between all cities) is O(n!)
Note
First find n
Simplify into psuedo-code till you just have loops
Examine them
(Basic test of fluency and understanding of your language of choice, like fizzbuzz)
There are also tools for this, which we'll get to later
Disclaimer: If you use this implementation in an interview, you will not get the job.
needle = '4'
haystack = [2, 8, 23, 5, 4, 7, 42]
idx = 0
while haystack[idx] < len(haystack):
if haystack[idx] == needle:
print "Found it at index " + str(idx)
idx += 1
Note
Let's say we're looking for "needle" in "haystack"
needle = '4'
haystack = [2, 8, 23, 5, 4, 7, 42]
idx = 0
while haystack[idx] < len(haystack):
if haystack[idx] == needle:
print "Found it at index " + str(idx)
idx += 1
n is len(haystack)
needle = '4'
haystack = [2, 8, 23, 5, 4, 7, 42]
idx = 0
while haystack[idx] < len(haystack):
if haystack[idx] == needle:
print "Found it at index " + str(idx)
idx += 1
Same disclaimer as before.
words = ['linux', 'washington', 'linux', 'festival']
idx = 0
while idx < len(words):
check = 0
while check < len(words):
if idx != check and words[check] == words[idx]:
print "found a repeated word!"
words = ['linux', 'washington', 'linux', 'festival']
idx = 0
while idx < len(words):
check = 0
while check < len(words):
if idx != check and words[check] == words[idx]:
print "found a repeated word!"
n is len(words)
words = ['linux', 'washington', 'linux', 'festival']
idx = 0
while idx < len(words):
check = 0
while check < len(words):
if idx != check and words[check] == words[idx]:
print "found a repeated word!"
words = ['linux', 'washington', 'linux', 'festival']
idx = 0
while idx < len(words):
check = 0
while check < len(words):
if idx != check and words[check] == words[idx]:
print "found a repeated word!"
Note
faster to sort the list (sorts can go very fast) then traverse once, comparing each item to the previous
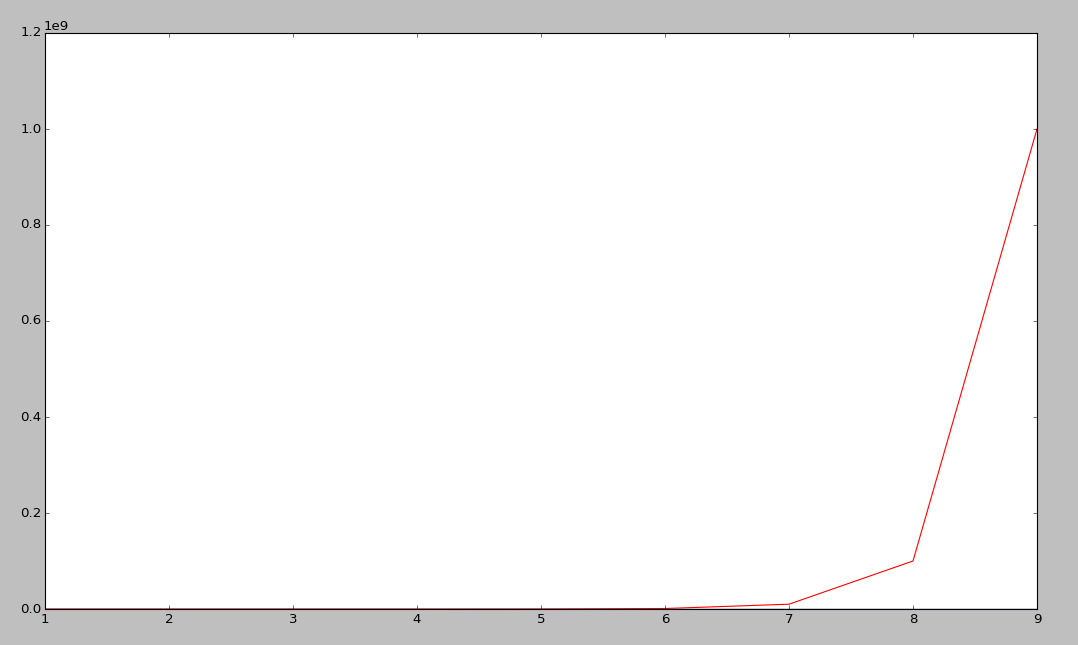
Note
This graphs a bunch of complexities:
Exponential is red (constant raised to the n)
Quadratic is black
Linear is cyan
nlogn is green
logarithmic is blue
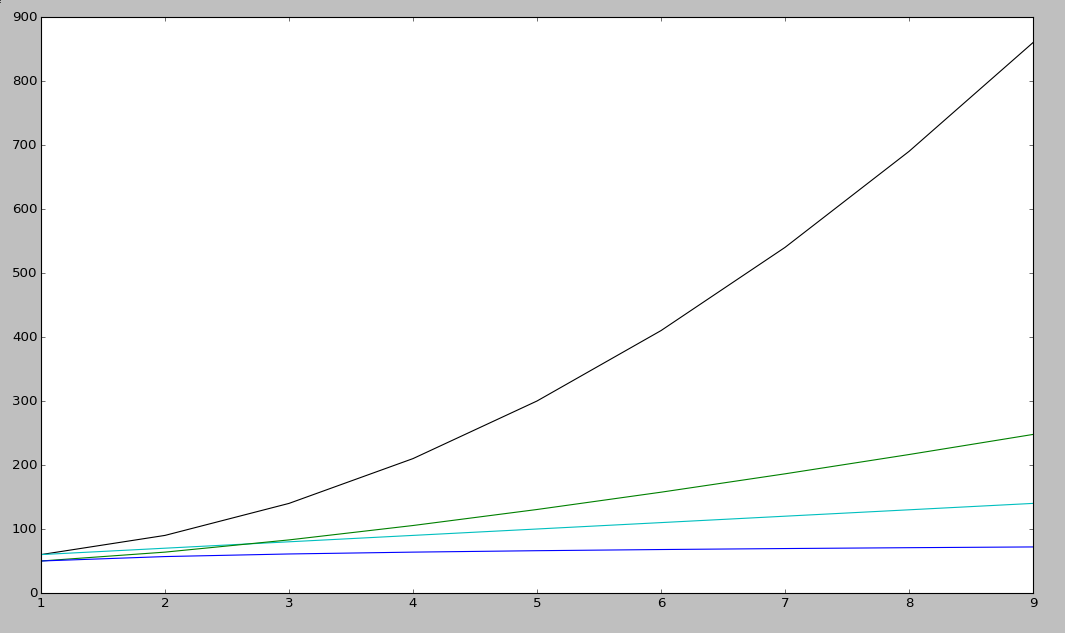
Note
Quadratic is black
Linear is cyan
nlogn is green
logarithmic is blue
def binary_search(l, value):
low = 0
high = len(l)-1
while low <= high:
mid = (low+high)//2
if l[mid] > value: high = mid-1
elif l[mid] < value: low = mid+1
else: return mid
return -1
def binary_search(l, value):
low = 0
high = len(l)-1
while low <= high:
mid = (low+high)//2
if l[mid] > value: high = mid-1
elif l[mid] < value: low = mid+1
else: return mid
return -1
def binary_search(l, value):
low = 0
high = len(l)-1
while low <= high:
mid = (low+high)//2
if l[mid] > value: high = mid-1
elif l[mid] < value: low = mid+1
else: return mid
return -1
Binary search is log(n)
"In mathematics, the logarithm of a number is the exponent to which another fixed value, the base, must be raised to produce that number."
big-oh is UPPER BOUND
big-omega is LOWER BOUND -- the program can never run faster than this
Big theta (not all programs will have this) is when upper and lower bounds match
If a slow operation is done infrequently, we can spread its cost over all the times it didn't happen...
def binary_search(l, value, low = 0, high = -1):
if not l:
return -1
if(high == -1): high = len(l)-1
if low == high:
if l[low] == value: return low
else:
return -1
mid = (low+high)//2
if l[mid] > value:
return binary_search(l, value, low, mid-1)
elif l[mid] < value:
return binary_search(l, value, mid+1, high)
else: return mid
how much memory does it take?
In-place sorting vs sorting by copying the array
Graphs of space complexity and show how they look quite a bit like time complexity
Note
TODO: sorting algos, in-place vs otherwise. example of very large arrays or very small memory, where this would actually matter
copy elements:
function reverse(a[0..n - 1])
allocate b[0..n - 1]
for i from 0 to n - 1
b[n − 1 − i] := a[i]
return b
vs in-place:
function reverse_in_place(a[0..n-1])
for i from 0 to floor((n-2)/2)
tmp := a[i]
a[i] := a[n − 1 − i]
a[n − 1 − i] := tmp
Constant times differ by several orders of magnitude.
Note
Grace Hopper and the Nanoseconds
metaphor: going to the fridge vs going to the store vs going to the moon
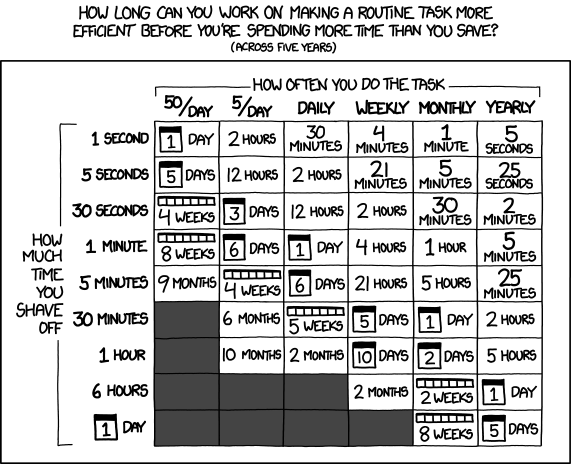
Note
Approximately last 15mins?
same things apply to saving time in your algorithm
Note
from cracking the coding interview, p. 56
Expected input size?
How much of test suite time is setup/teardown?
Note
TODO: tools/frameworks for mocking heavy load on a program Worst case vs expected case
Slow to perform vs slow to write
Note
Is speed the worst problem that it has right now?
What's the minimum that'll make your users happy?
What's the maximum past which your users won't notice improvements?
How long will it take the team to make the next big speedup...
It's probably not how you structured your algorithm. Or you fix the obvious algorithmic stupidity and it's still bad.
Remember the orders of magnitude thing?
Note
Note
"a slow program" could mean two things: code that's not performant, or code that takes forever to acutally get written. sometimes one is worse than the other.
Note
-- psuedo-code -- simplify it till all you have are bits that'll take constant time, and loops
Note
TODO: GRAPHS of high constant vs low constant, fast vs slow -- same graphs as before -- AGAIN, this is why context is critical
Note
TODO: sort them * specific vs general * automated vs manual * language-specific vs platform-agnostic
Each language has its own
Python: Run Snake Run
C: GDB/gprof
http://en.wikipedia.org/wiki/Instrumentation_%28computer_programming%29
accidentallyquadratic.tumblr.com
These slides are online at: